専門分野
位相幾何学,多様体間の写像の理論,大域的特異点論,投影による形状理解,科学教育
研究テーマ
- 写像による形状理解の基礎理論と応用
- 数学を活用するためのweb教材の開発,数学を身近に感じ探究心を育むための実践的教育
輪郭線によるかたちの理解(形状解析)
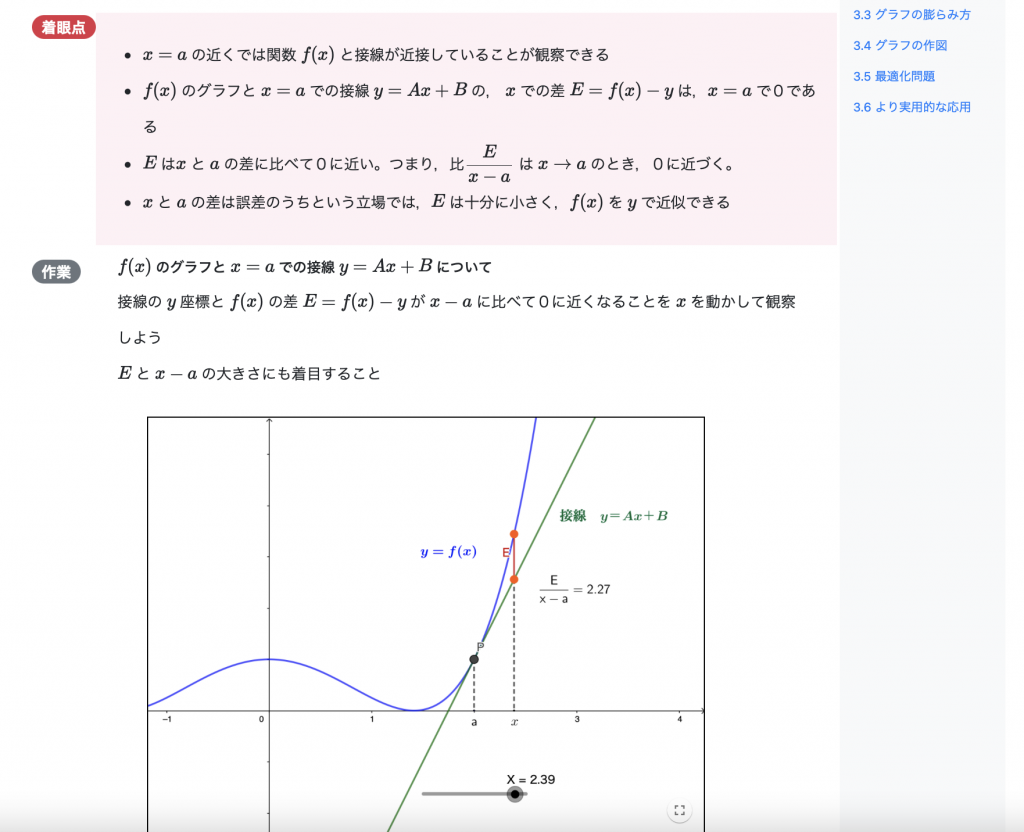
3次元空間の中に埋め込まれた曲面,例えばドーナツの表面を平面に投影すると輪郭線と呼ばれる線が現れます。実際に,曲面上の点を投影すると,様々な輪郭線が観察できます。(Torus_point_plot.html)
私たちは輪郭線を使って,曲面のかたちを紙の上にスケッチし,逆に,スケッチした輪郭線から曲面のかたちを推測しています。
もう少し詳しく説明しましょう。
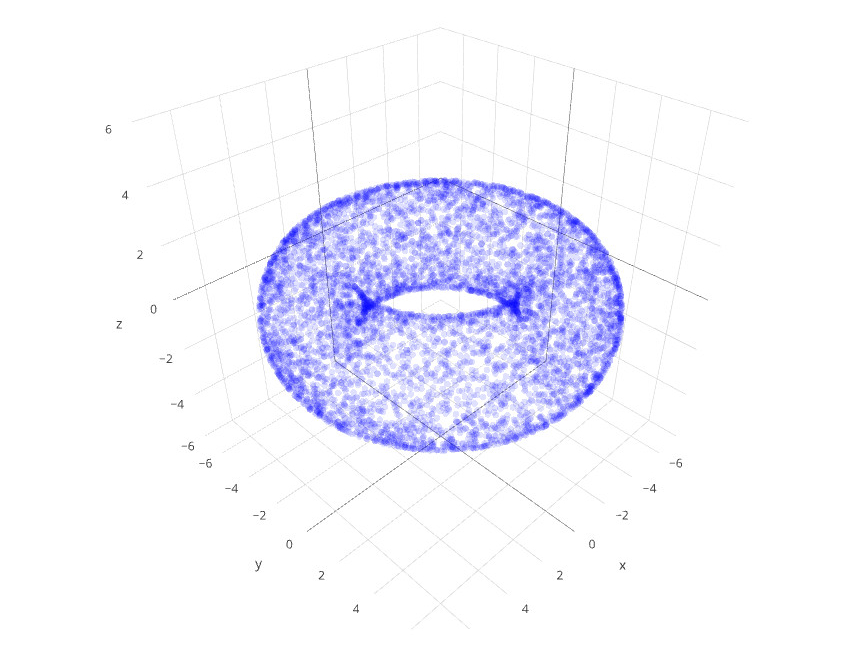
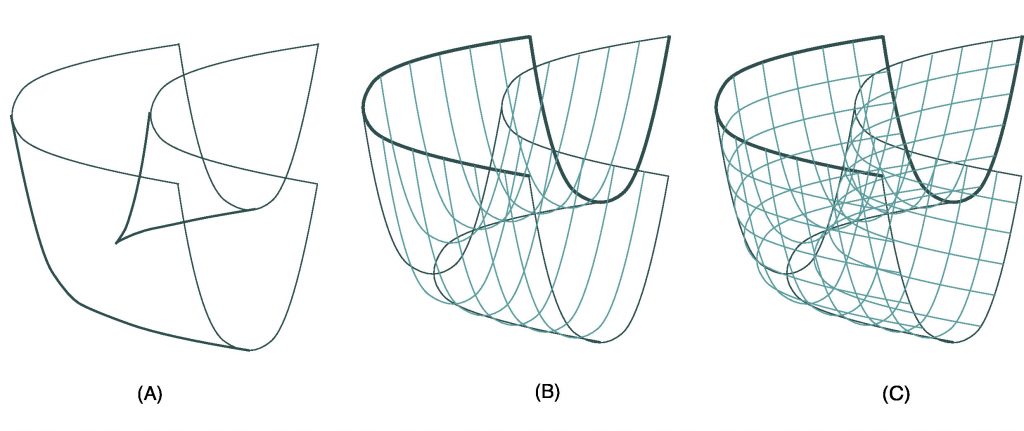
図1には,3次元空間に埋め込まれたトーラスの輪郭線(A)と,それを実現する2タイプの曲面が示してあります。(B)では輪郭線(A)に補助曲線を描きたして(D)の立体形状を復元していて,(C)では同じ輪郭線(A) から(E)のような立体形状を復元しています。一つの輪郭線から複数の立体形状が復元できるところに複雑さがありますが,復元された形状は,どちらも球面にパイプ(ハンドル)を接着したかたちであるところは同じです。こうしてみると,輪郭線は,かたちを完璧に復元することはできませんが,かたちについて何かを伝えています。輪郭線から曲面のかたちを推測することは,ロボット視覚(robot vision)をはじめ,工業部品の分別などの応用に繋がります。
多様体の可視化
目に見えない高次元のかたち(多様体という)を,投影と輪郭線を手がかりに推測することも重要な研究です(大域的特異点理論)。
たとえば,S 2 × S 2, S 2ט S 2(Hirzebruch の複素曲面)という4次元図形は,図1(A)と同じ輪郭線を持ちます。図1(A)は,球面に把手(とって)を付けたことを表現していますが,Hirzebruchの複素曲面も同じく,4次元球面に把手を付けたものだということが,この輪郭線から分かります。これは,目に見えない図形のかたちについての大きな情報です。また,(B) や(C) の補助線を2次元球面と考えると,これらの4次元図形の姿を捉えることができます。高次元になると,投影で失われる情報も多いのですが,それでも輪郭線は,かたち(多様体)について何かを伝えています。ときには失われた情報のいくつかを加えて様子を見ながら,輪郭線がかたちについて何を伝えているのかを探るのが,輪郭線による形状理解という研究です。
可視化の利用
観測機器の発達により,現在では,多様な観測手法により多量のデータを採取することができます。これらのデータは,高次元空間の中に分布する点と考えられますが,その形を直接見ることはできません。それを可視化する(目に見える形,つまり3次元や2次元に投影して形を理解する)ことは重要な研究です。例えば,データの分布に「(高次元の)くぼみ」が発見できれば,そのくぼみの規模や位置の変化を追うことでデータから有益な傾向がつかめる可能性があります(そのためには,まず,くぼみとは何かを定式化する必要があります)。
輪郭線によるかたちの理解は,写像とその特異点,特異値集合(輪郭線を一般化したもの)を利用した可視化の研究とも言えます。
高次元のかたちの例
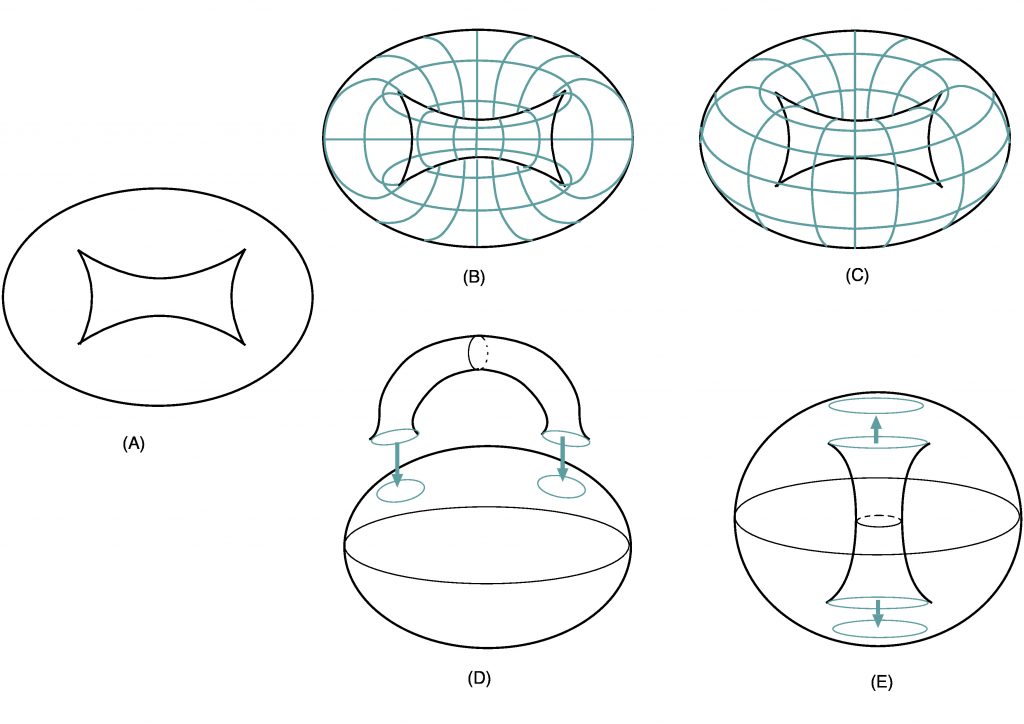
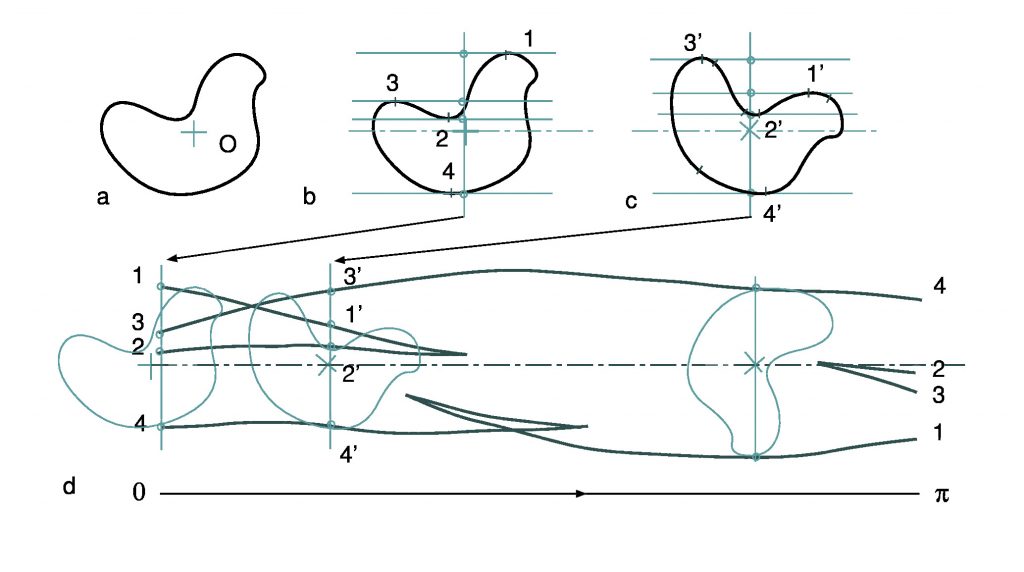
図2は,5次元の中の3次元図形(3次元射影空間という多様体)を平面に可視化した例で,(c),(d) はこの図形の輪郭線を表しています。この輪郭線は4面体の平面投影 (a), (b) と密接に関連していて,この図形の持つ対称性が輪郭線に反映されていることがわかります(弘前大学 山本稔との共同研究)。
図3は,紙を4つ折りにしようと曲げている最中の形を,2つの放物線をずらして重ね描きして表現したものです。投影と輪郭線という視点からこの形を研究し,高次元の「4つ折り」でも同じ現象が起きることを確認しました。高次元の折りたたみではどんな現象か起きるのかの探求自体も興味深いのですが,折りたたみの観察を重ねると,「積」多様体MxN という高次元の形の可視化が可能になるはずです。
そのほかの最近の研究テーマ(幾何学,応用関連)
数学・幾何学の手法や考え方は,幾何学そのものの理解だけでなく,実社会でも随所に応用できます。その例を示します。
■全周投影による形状解析
図4は,平面上のかたち(アヒル)を様々な方向に投影して,その輪郭線を調べてたものです。この方法で,これまでに曲線の変曲点や周長(Cauchy Crofton 定理),形の特徴量の間の関係式(Fabricius-Bjerre 公式)が復元できました。応用として偏西風の蛇行やくぼみの解析にも応用できそうです。
■Boy 曲面の再理解
古くから興味を持たれてきた Boy 曲面,Steiner 曲面という3次元空間内の曲面を,投影の手法を影に使い,より直接的に理解,再構成しました(図5)。4次元空間内の曲面を3次元空間に可視化したとも考えられます。
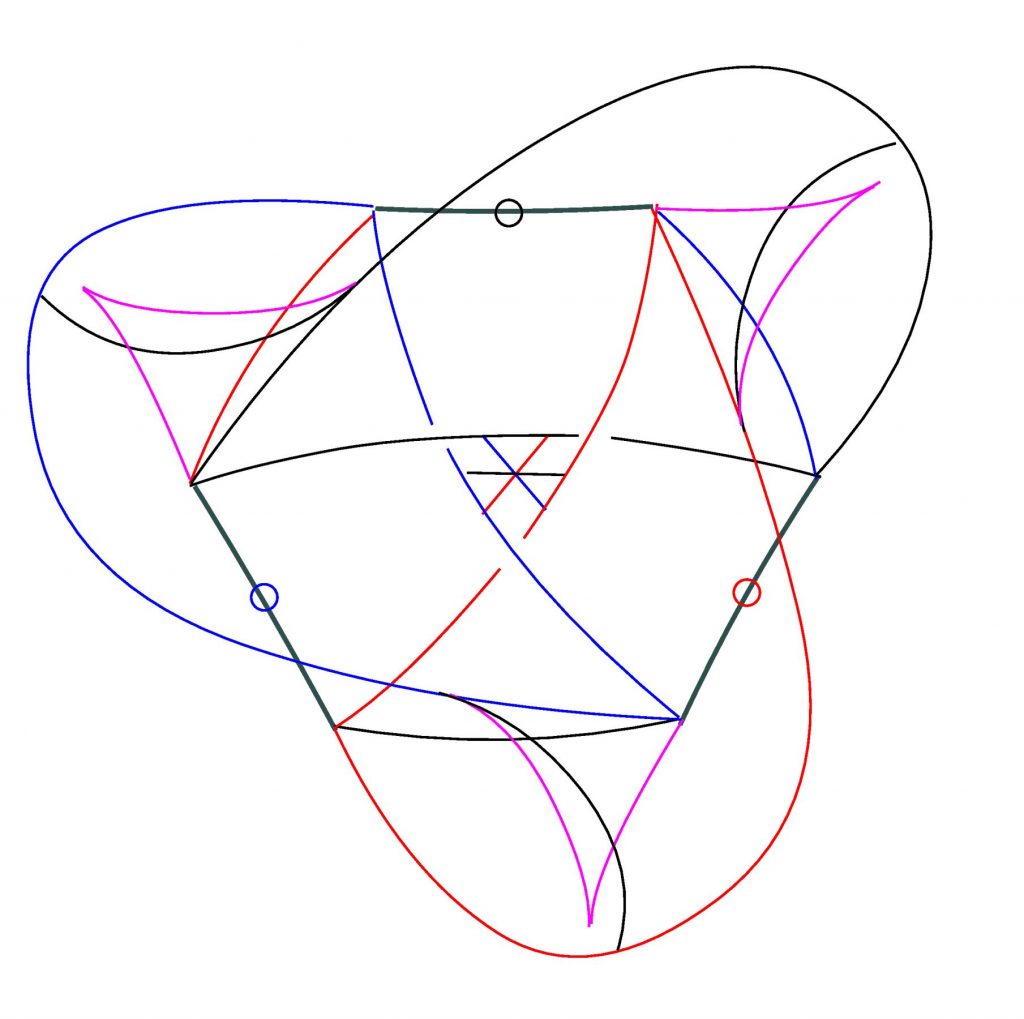
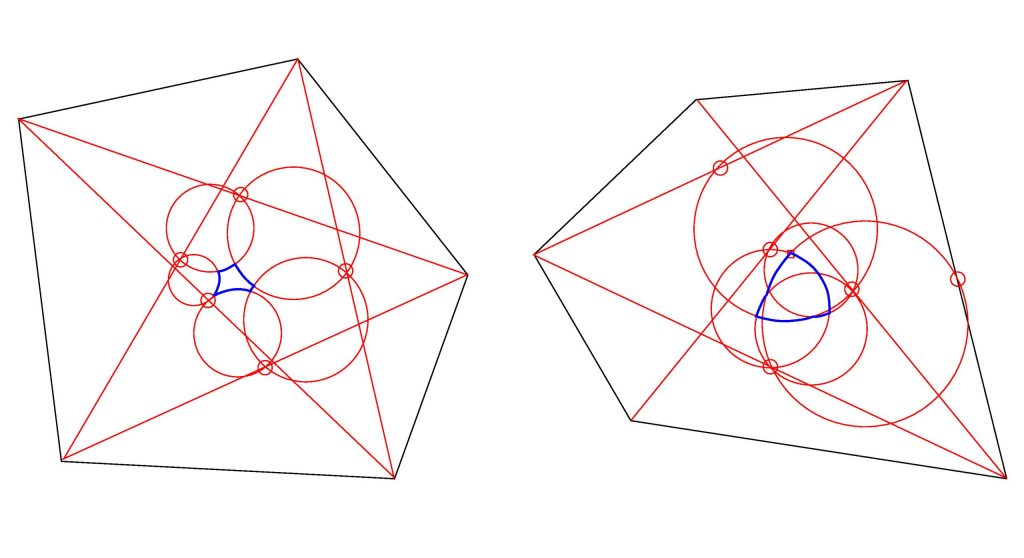
■多角形の回転中心の軌跡の解析(図6)
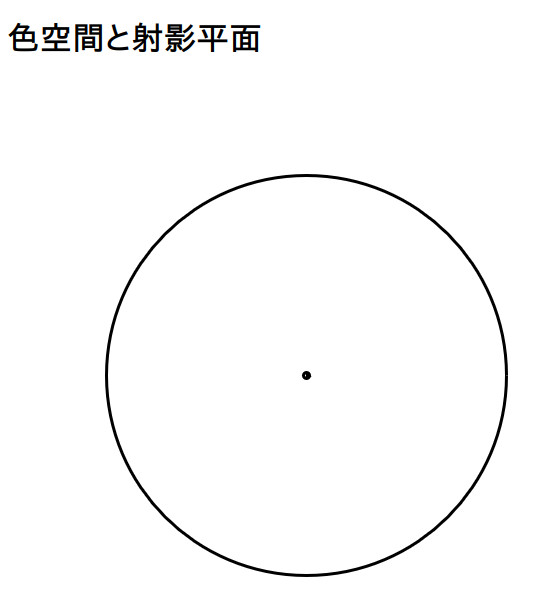
■色空間(RGB空間)の平面可視化
射影平面という幾何学で大切な曲面を利用して色空間を可視化してみました。円周上の対称点に「補色」の関係にある色が現れます(図7)。(color.html)
■色彩情報を利用した地上撮影の雲画像による天候判断
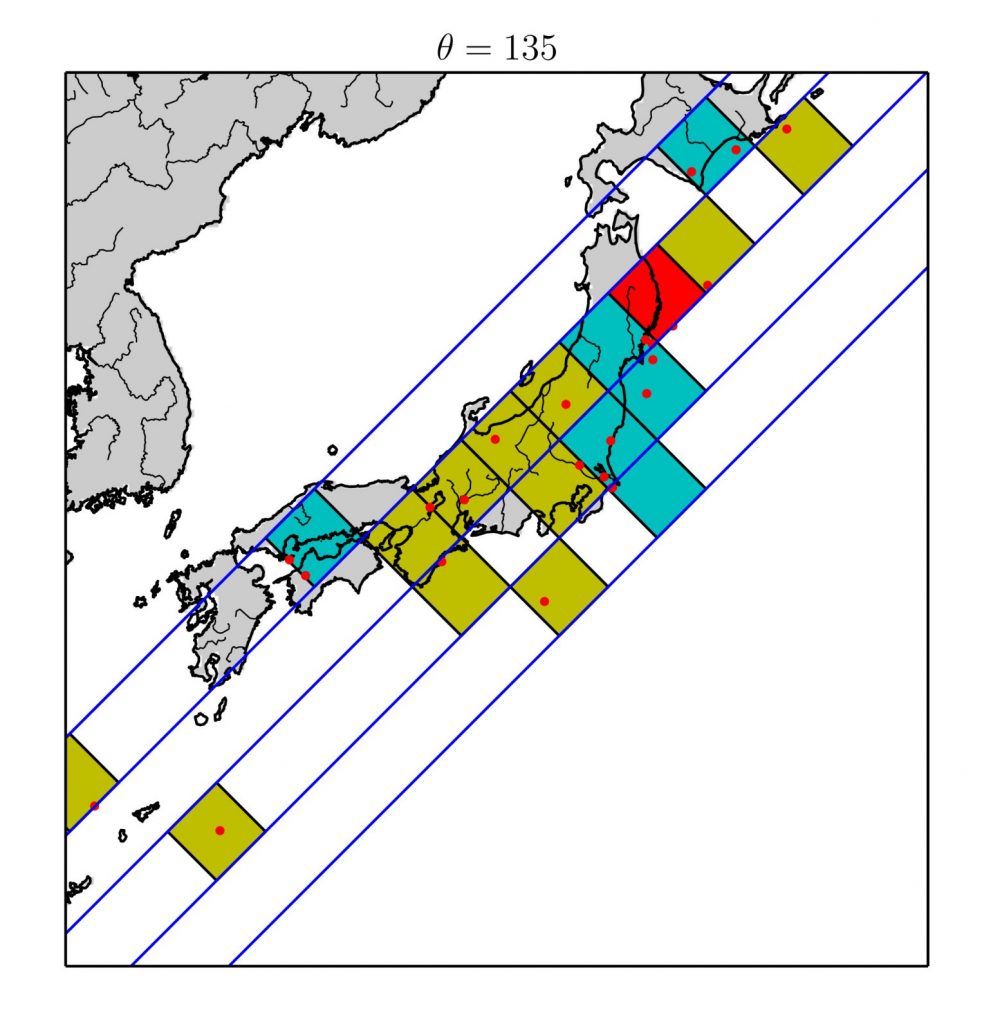
■日本列島で発生した地震震央の直線状配置の検出(図8)
そのほかの活動
高大接続センター 高大接続教育部門員として,高等学校で数学を身近に感じ,考える楽しさを体験してもらう授業(アカデミック授業)や,在学生に対する質問教室,テキストの編集や作成を行っています https://www.akita-u.ac.jp/kdcenter/