群知能アルゴリズム

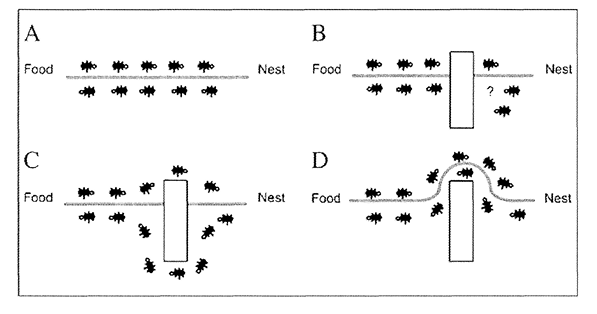
組合せ最適化問題を解決する群知能の研究も行っています。アリやハチなどの自然界の生物群の群行動を模倣した群知能を使うことで厳密な解を求めることが難しい組合せ最適化問題の近似解を効率良く求める研究です。群知能は人工知能の一つの分野と認識されていて、様々な組合せ最適化問題に応用されています。ハチやホタルの集団行動を模したアルゴリズムを施設配置問題に応用しました。

対戦ゲームとAI

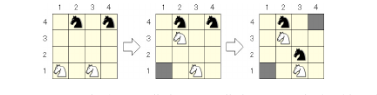
将棋や囲碁などのゲームではAIが人の能力を超えて強力になっています。対戦ゲームの理論では、モンテカルロ木探索という手法を用いて盤上ゲームにおける対戦プレイヤーをプログラムする研究も行っています。Knight-Amazon という盤上ゲームを提案し、必勝戦略が存在するケースを解明しました。

新しいオートマトンのモデル

代数学、離散数学、グラフ理論と強い関連を持つのがコンピュータサイエンスの研究です。チューリングマシンやオートマトンといった構造は計算機の理論的モデルとして活用さえています。形式言語理論はプログラミング言語などの機械語をモデル化することに役立つ理論です。オートマトンは受理できる言語の豊富さによりその能力が決まります。

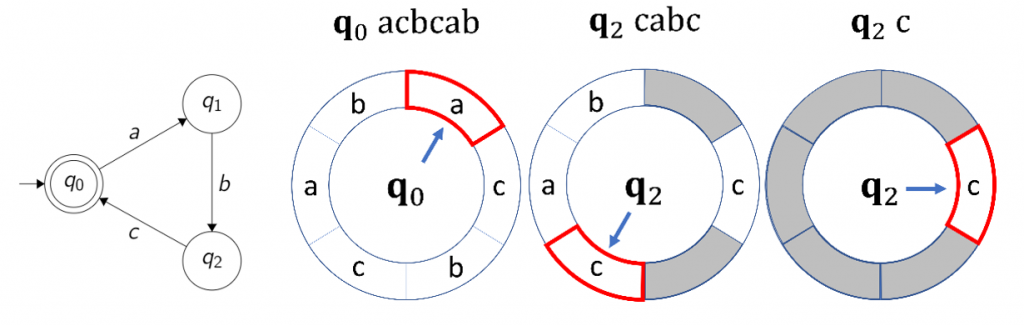
有限オートマトンやプシュダウンオートマトンの読み取りヘッドの振る舞いを変更することで言語受理能力がどのように影響を与えるのか興味を持っており、一方向性ジャンピングオートマトンの概念を提案して解析しています。

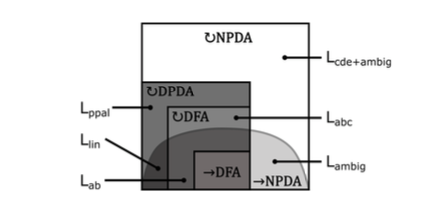
より強力な機械モデル（双方向オートマトン、プッシュダウンオートマトン、線形有界オートマトンなど）への処理モードの拡張を研究しました。シミュレーションと分離の結果を通じて、言語クラスの階層を確立しました。

折畳みシステム

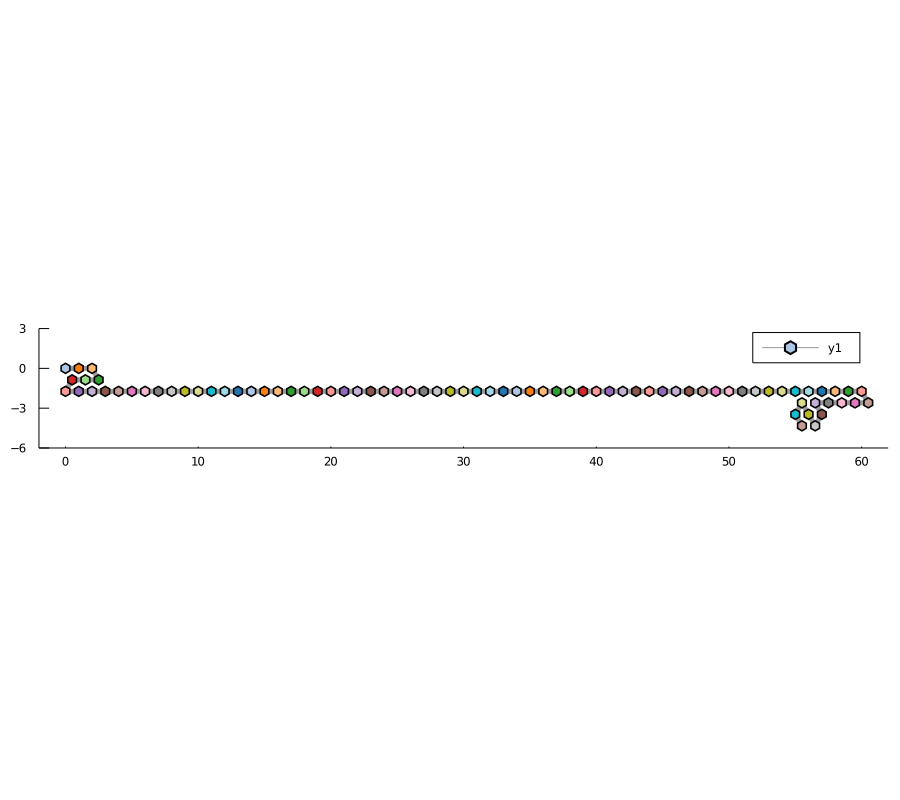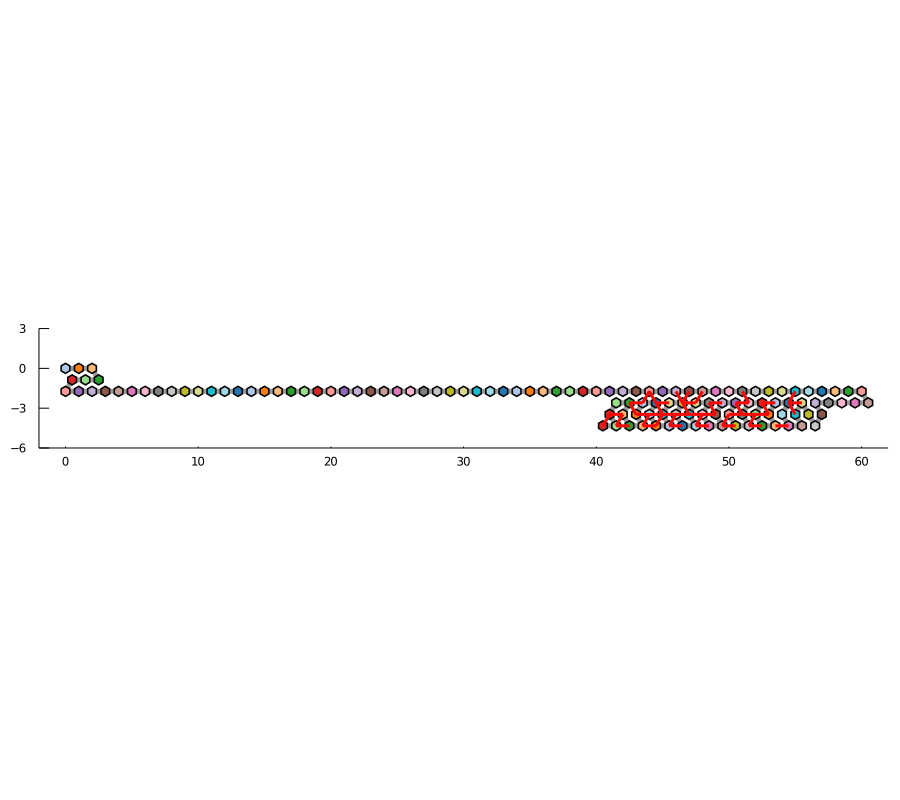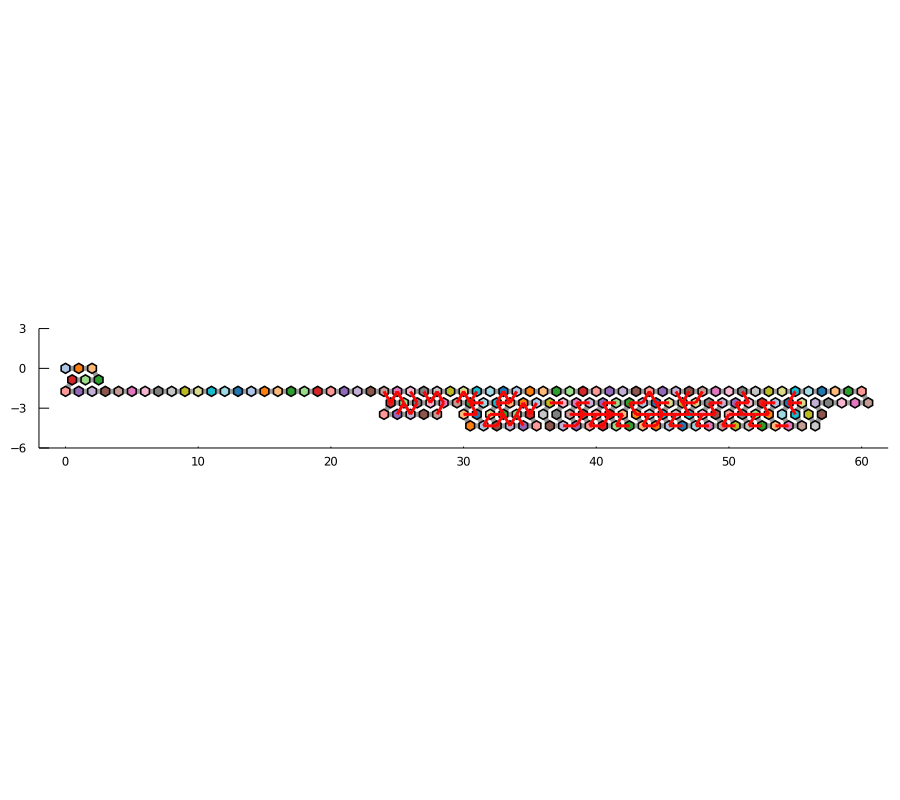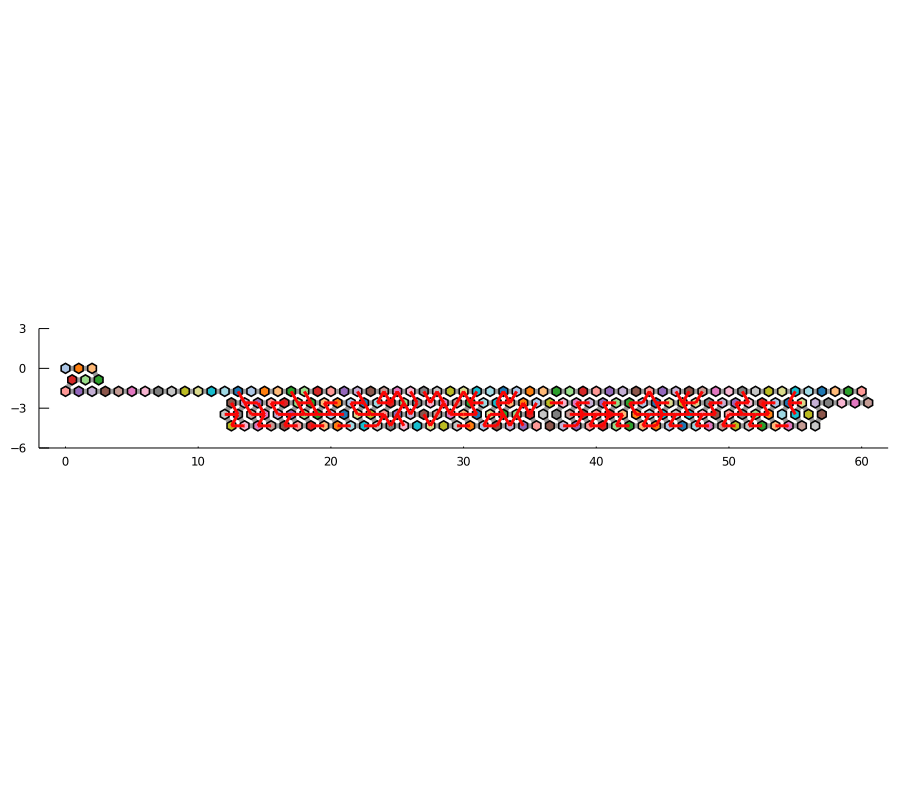
折畳みシステムは、生物内のRNA分子の共転写的折り畳みをモデル化します。このモデルを使用して、所望の形状に折り畳まれる抽象的なRNA配列を構築しています。これは基本的に、RNAの折り畳みを「プログラム」してカウンターや長方形のような単純な形状を実現する方法です。

反復のカウント

特定の長さの文字列に含まれる異なる反復の最大数を見つけることを目指しています。私たちの方法は、その文字列内の反復の開始位置（接尾辞をアルファベット順に並べたもの）に基づく間隔を見て、それらの間隔がどのようにネストされるかを分析することです。