立方体数独

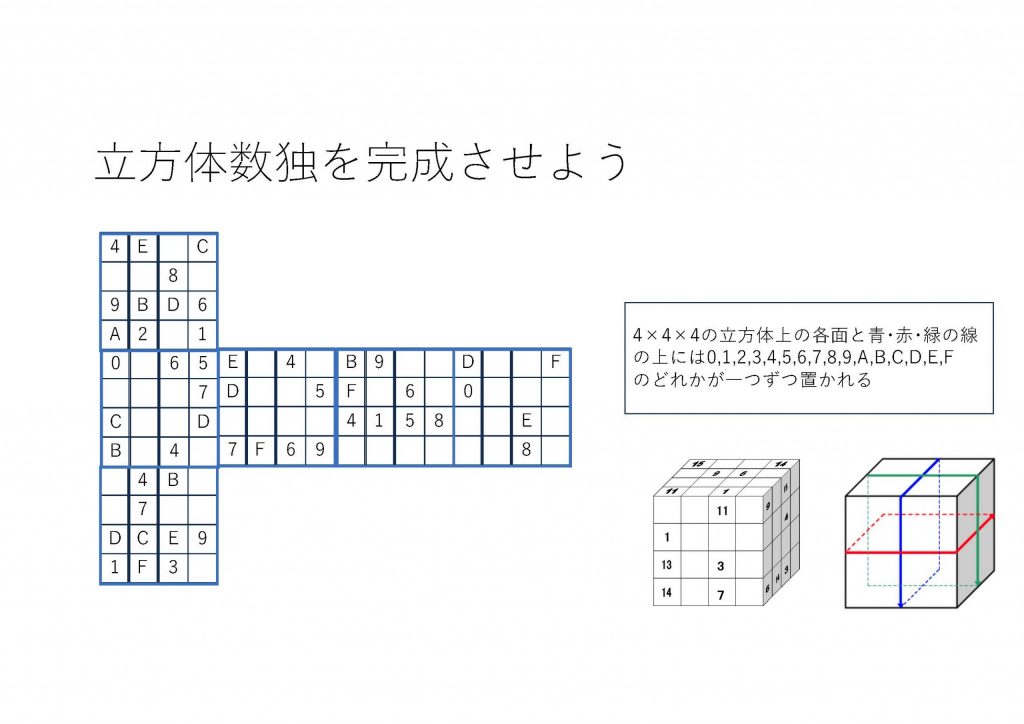
組合せ構造の研究として、ラテン立方体と正則3部グラフと関連する組合わせデザインの関係を調べています。正則3部グラフが完全1-因子分解を持つケースを解析しています。2次のラテン方陣の総数を計算機実験で求める研究も実施しています。ラテン立方体はラテン方陣を立方体の表面に拡張したものです。ラテン立方体を基に数独のようなパズルを作る事もできます。

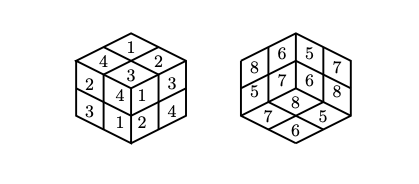
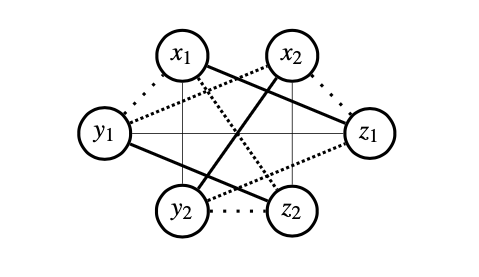
立方体上の組み合わせ構造を調査する研究は８クイーン問題を立方体上に拡張することから始まりました。８クイーン問題とは、チェスの盤上に、８個のクイーンをどのコマも互いに当たりがない配置を求めることである。nクイーン問題とnルーク問題を立方体上で考察しました。群論のCauchy-Frobeniusの定理を応用しています。

亜群の作用：１５パズル

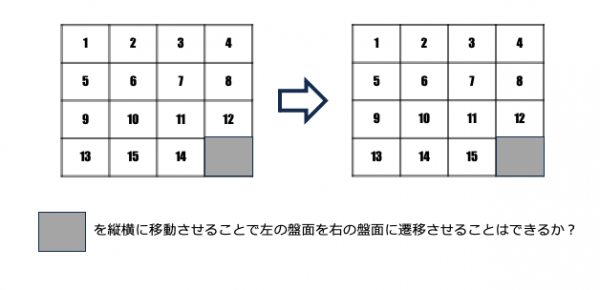
また15パズルにおいて群の作用が解決の鍵となりますが、パンケーキソート問題を2次元に拡張した際には群ではなく亜群の偏作用の概念が必要になります。亜群と偏作用の概念の理解を目的とした研究も大きなテーマの一つです。詳しくはこちらを参照してください。