組合せ群論

群、半群（特に逆半群）、亜群（Groupoid）の有限表示と代数的構造の解明、そして、関連する語の問題やその他のアルゴリズム問題に取り組んでいます。無限群や無限半群は構造が分かりにくいものですが、幾何学的な構造を利用することで効率的なアルゴリズムを構築することが出来る場合があります。自由群、自由積、融合積、HNN拡大などの組合せ群論・幾何学群論における重要概念とBass -Serre理論との関連に興味を持っています。

幾何学群論

グラフや組合せ構造を用いた手法だけでなくvan Kampen ダイアグラムと呼ばれる幾何学的手法を用いることでアルゴリズム問題の可解性・決定性やその計算効率を研究しています。アルゴリズム問題の可解性・決定性はロジック（数理論理学）の研究分野でもあり、代数学、論理学、グラフ理論など多様な手法を駆使する研究となります。

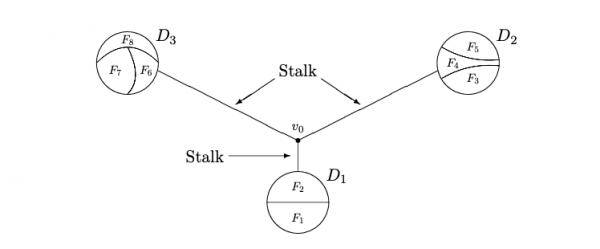
逆半群と亜群

逆半群と亜群による局所的な対称性と偏作用は数学において様々な応用がありますが、群の作用と比べるとはるかに難しいものですが、研究対象として最も興味を持っています。結晶構造は群によって規定できますが、ペンローズタイリングのような構造の解析に群は適しません。代数系に幾つかの応用を発見しています。