輪郭線によるかたちの研究

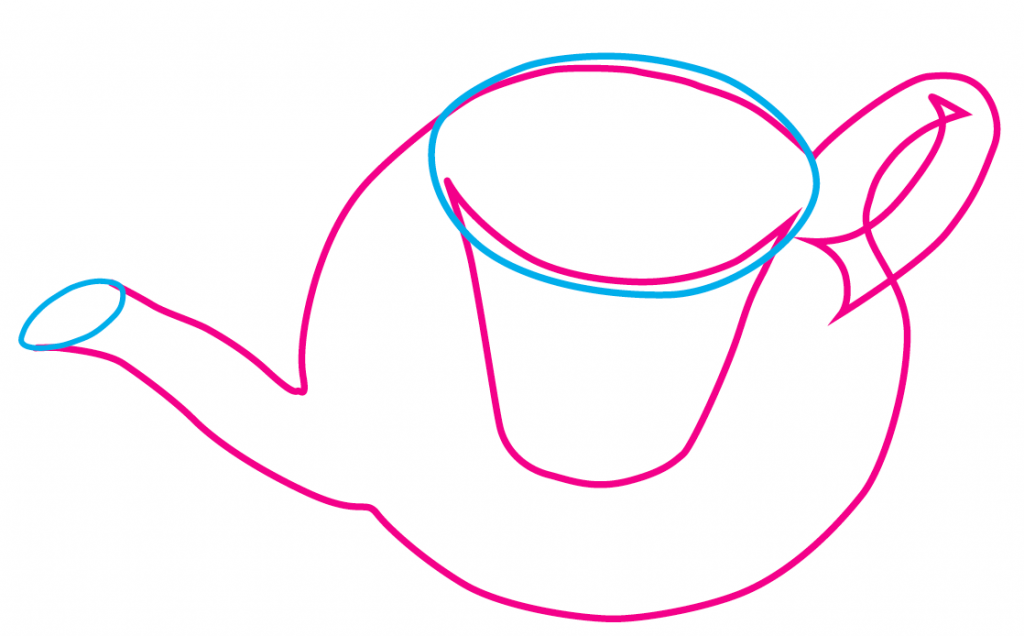
3次元空間の中にある曲面を平面に投影すると輪郭線と呼ばれる線が現れます（図1，ポットの輪郭線）。私たちは，曲面を輪郭線を使ってスケッチし，またそのスケッチから曲面のかたちを推測しています（図2）。輪郭線による曲面のかたちの推測は，ロボット視覚（robot vision）や，工業部品の分別などの応用に繋がります。

多様体の可視化

直接目にすることができない高次元のかたち（多様体という）を，投影と輪郭線を手がかりに推測することも重要な研究です（大域的特異点理論）。

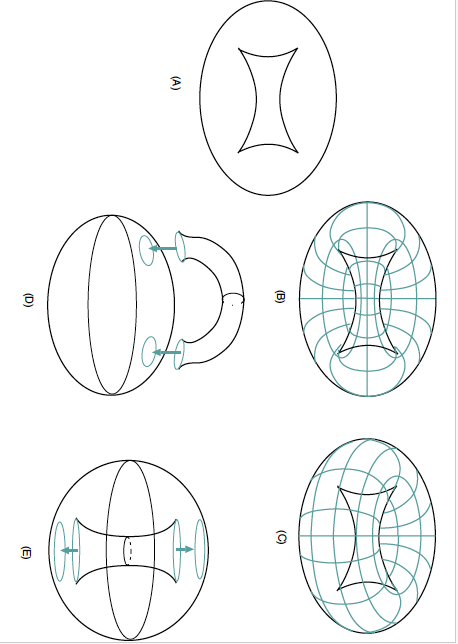
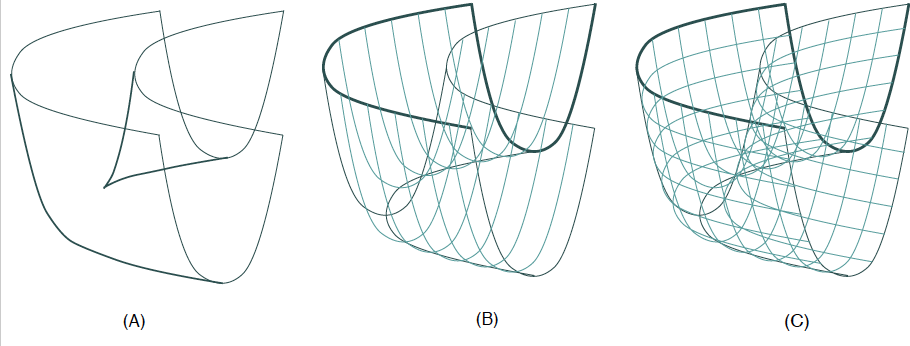
図3は，紙を4つ折りにする途中の形を表現したものです。高次元の「4つ折り」でも同じ輪郭線が発生することが確認でき，この折りたたみは，高次元「積」多様体　MxN を可視化する際の道具として有力な候補です。

ケルト結び目模様

ケルト文化の伝統的なシンボルとして、ケルト模様と呼ばれる模様、デザインがあります。これはとても綺麗な模様ですが、このデザインを数学的に扱い、どんな特徴があるのか、人が綺麗と思うのはどんな時なのか、などを研究します

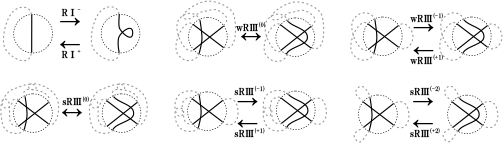
射影図に対する局所変形

•ヒモを1本用意しよう。このヒモを適当にからめて、

•その両端を繋いだものを結び目といいます

•（数学の言葉で言うと、S^1のS^3への埋め込み）。

•複数（1本も含む）のヒモをからめて各々のヒモの両端点を繋いだものを絡み目といいます。

•本研究では結び目や絡み目、空間グラフの影である射影図に対してさまざまな局所変形を許した同値類はどんなものなのか（不変量は何か、どのような量が変化するのか）についての研究を行っています